Il est important de connaitre la différence entre la progression arithmétique et géométrique, car si elles sont confondues, les résultats de certains calculs peuvent être faussés. Nous les retrouvons dans les métiers de la balistique comme les spotters des tireurs mais aussi dans les métiers du spatial.

Pour rappel, la progression arithmétique est une suite de nombres avec une différence égale nommée « raison ».
Par exemple, dans la suite 2 ;4 ;6 ;8 ;10, la raison est 2. Dans ce cas, la pente est positive, mais elle peut être négative si la raison est négative.
Dans le cas de la progression géométrique, nous n’additionnons pas la raison, mais nous multiplions par un facteur constant.
Par exemple 2 ; 4 ; 8 ; 16 ; 32… Là aussi, la courbe peut être positive ou négative en fonction du facteur.
Considérons un tir balistique d’un artilleur (je schématise pour l’exemple volontairement, il n’est pas nécessaire à ce stade de démonstration et de prendre en considération toutes les lois qui régissent la trajectoire d’un obus). La courbe du projectile sera, en premier temps sous forme de progression arithmétique puis quand la balle n’aura plus assez de cinétique, la courbe sera sous forme de progression géométrique.
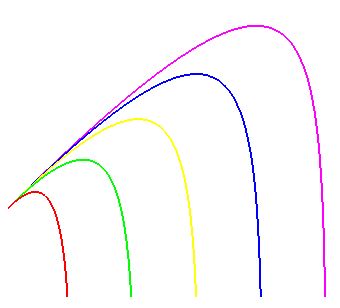
Nous pouvons considérer que la première partie de la trajectoire du tir est « rectiligne » et que la seconde partie, soumise à des forces comme la gravité et la friction de l’air, prend la forme d’une courbe.
Dans le calcul de la trajectoire d’un tir balistique, en fonction de la distance de la cible, on considérera la trajectoire comme une progression arithmétique, géométrique ou les deux.
